PRML - Lab 2: FNN 模型

本次作业完成了选题 1 的实验内容，利用 NumPy 实现了一个 FNN 模型，并在 MNIST 数据集上进行了训练。

Pattern Recognition and Machine Learning (H) @ Fudan University, spring 2021.

实验简介

实验报告

1 FNN 算子的反向传播

1.1 Matmul

1.1.1 公式推导

输入一个 $n\times d$ 的矩阵 $X$ 和一个 $d\times d’$ 的矩阵 $W$，算子 Matmul 的正向传播公式为：

$$ Y = X\times W \tag{1.1} $$

输出一个 $n\times d’$ 的矩阵 $Y$。

对于梯度的反向传播，有

$$ \nabla z = ( \frac{\partial z}{\partial X}_{n\times d}, \frac{\partial z}{\partial W}_{d\times d’} ) \tag{1.2} $$

我们利用向量化（vectorization）进行对矩阵求导的求解：

$$ \begin{align} \mathit{vec}(\frac{\partial z}{\partial X}_{n\times d}) &={(\frac{\partial Y}{\partial X})^T}_{nd\times {nd’}} \times {\mathit{vec}(\frac{\partial z}{\partial Y})}_{nd’} \\ &={({\frac{\partial {\mathit{vec}(X\times W)}_{nd’}} {\partial {\mathit{vec}(X)}_{nd}}})^T}_{nd\times {nd’}} \times {\mathit{vec}(\frac{\partial z}{\partial Y})}_{nd’} \\ &={({\frac {\partial ({\mathit{vec}(X)}_{nd} \times {(I_n\otimes W)}_{nd\times {nd’}})} {\partial {\mathit{vec}(X)}_{nd}} })^T}_{nd\times {nd’}} \times {\mathit{vec}(\frac{\partial z}{\partial Y})}_{nd’} \\ &={(I_n\otimes W)}_{nd\times {nd’}} \times {\mathit{vec}(\frac{\partial z}{\partial Y})}_{nd’} \\ &=\mathit{vec}({(\frac{\partial z}{\partial Y}\times W^T)}_{n\times d}) \end{align} \tag{1.3} $$

这里 $\mathit{vec}(X_{m\times n})$ 表示向量

$$ \begin{bmatrix} x_{11} & x_{12} & … & x_{1n} && … && x_{m1} & x_{m2} & … & x_{mn} \end{bmatrix} \tag{1.3.1} $$

$\otimes$ 表示 Kronecker 积，下标表示矩阵或向量的维度。

因此有

$$ \frac{\partial z}{\partial X}_{n\times d} = {(\frac{\partial z}{\partial Y}\times W^T)}_{n\times d} \tag{1.4} $$

类似 $(1.3)$ 的推导，同理可得

$$ \frac{\partial z}{\partial W}_{d\times d’} = {(X^T\times \frac{\partial z}{\partial Y})}_{d\times d’} \tag{1.5} $$

1.1.2 代码实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

# numpy_fnn.py

class Matmul(NumpyOp):
    '''
    Matrix multiplication unit.
    '''

    def forward(self, x: np.ndarray, w: np.ndarray) -> np.ndarray:
        '''
        Args:
            x: shape(N, d)
            w: shape(d, d')

        Returns:
            shape(N, d')
        '''

        self.memory['x'] = x
        self.memory['w'] = w
        return np.matmul(x, w)

    def backward(self, grad_y: np.ndarray) -> Tuple[np.ndarray, np.ndarray]:
        '''
        Args:
            grad_y: shape(N, d')

        Returns:
            grad_x: shape(N, d)
            grad_w: shape(d, d')
        '''

        x: np.ndarray = self.memory['x']
        w: np.ndarray = self.memory['w']
        grad_x: np.ndarray = np.matmul(grad_y, w.T)
        grad_w: np.ndarray = np.matmul(x.T, grad_y)
        return grad_x, grad_w

1.2 Relu

1.2.1 公式推导

输入一个 $n\times d$ 的矩阵 $X$，对于 $X$ 中的每个元素 $X_{ij}$，算子 Relu 的正向传播公式为：

$$ Y_{ij} = \begin{cases} X_{ij} &(X_{ij} > 0) \\ 0 &(X_{ij}\le 0) \end{cases} \tag{2.1} $$

输出一个 $n\times d$ 的矩阵 $Y$。

对于梯度的反向传播，有

$$ \begin{align} \nabla z &=\frac{\partial z}{\partial X}_{n\times d} \\ &=\frac{\partial z}{\partial Y}_{n\times d} \odot \frac{\partial Y}{\partial X}_{n\times d} \end{align} \tag{2.2} $$

这里 $\odot$ 表示 Hadamard 积，即逐元素（element-wise）乘积。

其中，对于 $\frac{\partial Y}{\partial X}_{n\times d}$ 中的每个元素 ${Y’}_{ij}$，由 $(2.1)$ 有

$$ {Y’}_{ij} = \begin{cases} 1 &(X_{ij} > 0) \\ 0 &(X_{ij}\le 0) \end{cases} \tag{2.3} $$

因此，对于 $\frac{\partial z}{\partial X}_{n\times d}$ 中的每个元素 ${Z’}_{ij}$，令 ${Z_Y}’ = \frac{\partial z}{\partial Y}_{n\times d}$，由 $(2.2)$ 有

$$ {Z’}_{ij} = \begin{cases} {({Z_Y}’)}_{ij} &(X_{ij} > 0) \\ 0 &(X_{ij}\le 0) \end{cases} \tag{2.4} $$

1.2.2 代码实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

# numpy_fnn.py

class Relu(NumpyOp):
    '''
    Rectified Linear Unit.
    '''

    def forward(self, x: np.ndarray) -> np.ndarray:
        '''
        Args:
            x: shape(N, d)

        Returns:
            shape(N, d)
        '''

        self.memory['x'] = x
        return np.where(x > 0, x, 0)

    def backward(self, grad_y: np.ndarray) -> np.ndarray:
        '''
        Args:
            grad_y: shape(N, d)

        Returns:
            shape(N, d)
        '''

        x: np.ndarray = self.memory['x']
        return np.where(x > 0, grad_y, 0)

1.3 Log

1.3.1 公式推导

输入一个 $n\times d$ 的矩阵 $X$，对于 $X$ 中的每个元素 $X_{ij}$，算子 Log 的正向传播公式为：

$$ Y_{ij} = \log X_{ij} \tag{3.1} $$

输出一个 $n\times d$ 的矩阵 $Y$。

对于梯度的反向传播，有

$$ \begin{align} \nabla z &=\frac{\partial z}{\partial X}_{n\times d} \\ &=\frac{\partial z}{\partial Y}_{n\times d} \odot \frac{\partial Y}{\partial X}_{n\times d} \end{align} \tag{3.2} $$

其中，对于 $\frac{\partial Y}{\partial X}_{n\times d}$ 中的每个元素 ${Y’}_{ij}$，由 $(3.1)$ 有

$$ {Y’}_{ij} = \frac{1}{X_{ij}} \tag{3.3} $$

因此，对于 $\frac{\partial z}{\partial X}_{n\times d}$ 中的每个元素 ${Z’}_{ij}$，令 ${Z_Y}’ = \frac{\partial z}{\partial Y}_{n\times d}$，由 $(3.2)$ 有

$$ {Z’}_{ij} = \frac{{({Z_Y}’)}_{ij}}{X_{ij}} \tag{3.4} $$

1.3.2 代码实现

为了防止 $X_{ij} = 0$ 时出现 $\log X_{ij}\rightarrow -\infty$ 导致溢出，这里我们给 $X_{ij}$ 附加了一个 $\epsilon = 10^{-12}$ 的修正。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

# numpy_fnn.py

class Log(NumpyOp):
    '''
    Natural logarithm unit.
    '''

    def forward(self, x: np.ndarray) -> np.ndarray:
        '''
        Args:
            x: shape(N, d)

        Returns:
            shape(N, d)
        '''

        self.memory['x'] = x
        return np.log(x + self.epsilon)

    def backward(self, grad_y: np.ndarray) -> np.ndarray:
        '''
        Args:
            grad_y: shape(N, d)

        Returns:
            shape(N, d)
        '''

        x: np.ndarray = self.memory['x']
        return grad_y / x

1.4 Softmax

1.4.1 公式推导

输入一个 $n\times d$ 的矩阵 $X$，对于 $X$ 中的每个元素 $X_{ij}$，算子 Softmax 的正向传播公式为：

$$ Y_{ij} = \frac{e^{X_{ij}}}{\sum\limits_{k=1}^d e^{X_{ik}}} \tag{4.1} $$

输出一个 $n\times d$ 的矩阵 $Y$。

对于梯度的反向传播，有

$$ \nabla z = \frac{\partial z}{\partial X}_{n\times d} \tag{4.2} $$

其中，对于 $\frac{\partial z}{\partial X}_{n\times d}$ 中的每个元素 ${Z’}_{ij}$ 有

$$ \begin{align} {Z’}_{ij} &=\frac{\partial z}{\partial X_{ij}} \\ &={(\frac{\partial z}{\partial Y_i})}_d \cdot {(\frac{\partial Y_i}{\partial X_{ij}})}_d \\ &=\frac{\partial z}{\partial Y_{ij}} \cdot \frac{\partial Y_{ij}}{\partial X_{ij}} + \sum\limits_{k=1,\,k\ne j}^d \frac{\partial z}{\partial Y_{ik}} \cdot \frac{\partial Y_{ik}}{\partial X_{ij}} \\ &=\frac{\partial z}{\partial Y_{ij}} \cdot \frac{\partial}{\partial X_{ij}}(\frac{e^{X_{ij}}}{\sum\limits_{t=1}^d e^{X_{it}}}) + \sum\limits_{k=1,\,k\ne j}^d \frac{\partial z}{\partial Y_{ik}} \cdot \frac{\partial}{\partial X_{ij}}(\frac{e^{X_{ik}}}{\sum\limits_{t=1}^d e^{X_{it}}}) \\ &=\frac{\partial z}{\partial Y_{ij}} \cdot \frac{e^{X_{ij}}}{\sum\limits_{t=1}^d e^{X_{it}}} \cdot (1 - \frac{e^{X_{ij}}}{\sum\limits_{t=1}^d e^{X_{it}}}) - \sum\limits_{k=1,\,k\ne j}^d \frac{\partial z}{\partial Y_{ik}} \cdot \frac{e^{X_{ij}}}{\sum\limits_{t=1}^d e^{X_{it}}} \cdot \frac{e^{X_{ik}}}{\sum\limits_{t=1}^d e^{X_{it}}} \\ &=\frac{\partial z}{\partial Y_{ij}}\cdot Y_{ij}\cdot (1 - Y_{ij}) - \sum\limits_{k=1,\,k\ne j}^d \frac{\partial z}{\partial Y_{ik}}\cdot Y_{ij}\cdot Y_{ik} \\ &=Y_{ij}\cdot ( \frac{\partial z}{\partial Y_{ij}} - \sum\limits_{k=1}^d \frac{\partial z}{\partial Y_{ik}}\cdot Y_{ik} ) \end{align} \tag{4.3} $$

1.4.2 代码实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

# numpy_fnn.py

class Softmax(NumpyOp):
    '''
    Softmax over last dimension.
    '''

    def forward(self, x: np.ndarray) -> np.ndarray:
        '''
        Args:
            x: shape(N, d)

        Returns:
            shape(N, d)
        '''

        y: np.ndarray = np.exp(x) / np.exp(x).sum(axis=1)[:, None]
        self.memory['y'] = y
        return y

    def backward(self, grad_y: np.ndarray) -> np.ndarray:
        '''
        Args:
            grad_y: shape(N, d)

        Returns:
            shape(N, d)
        '''

        y: np.ndarray = self.memory['y']
        return y * (grad_y - (grad_y * y).sum(axis=1)[:, None])

2 函数 mini_batch 实现

我们使用 NumPy 重写了函数 mini_batch，用于之后的训练。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# numpy_mnist.py

def mini_batch(dataset: List[Tuple[Any, int]], batch_size=128) -> np.ndarray:
    '''
    Align the data and labels from the given dataset into batches.

    Args:
        dataset: the given dataset
        batch_size: the size of retrieved data

    Returns:
        Batches of [data, labels] pair.
    '''

    data: np.ndarray = np.array([np.array(pair[0]) for pair in dataset])
    labels: np.ndarray = np.array([pair[1] for pair in dataset])

    # Shuffle the dataset
    size: int = len(dataset)
    indices: np.ndarray = np.arange(size)
    np.random.shuffle(indices)

    batches: List[Tuple[np.ndarray, np.ndarray]] = []
    for i in range(0, size, batch_size):
        chunk: np.ndarray = indices[i:i+batch_size]
        batches.append((data[chunk], labels[chunk]))
    return batches

3 实验过程与结果

执行以下命令开始训练。

1

python ./numpy_mnist.py

3.1 实验 1

3.1.1 参数

1
2
3

epoch_number = 3
batch_size = 128
learning_rate = 0.1

3.1.2 预测准确率

1
2
3

[0] Accuracy: 0.9485
[1] Accuracy: 0.9647
[2] Accuracy: 0.9715

3.1.3 损失函数值

3.2 实验 2

这次，我们调大训练轮数（epoch_number），观察预测准确率的变化。

3.2.1 参数

1
2
3

epoch_number = 10
batch_size = 128
learning_rate = 0.1

3.2.2 预测准确率

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

[0] Accuracy: 0.9496
[1] Accuracy: 0.9600
[2] Accuracy: 0.9675
[3] Accuracy: 0.9761
[4] Accuracy: 0.9755
[5] Accuracy: 0.9775
[6] Accuracy: 0.9791
[7] Accuracy: 0.9795
[8] Accuracy: 0.9781
[9] Accuracy: 0.9810

可见，训练轮数越多，预测准确率越高，但到达一定准确率后开始波动，不再明显上升。

3.2.3 损失函数值

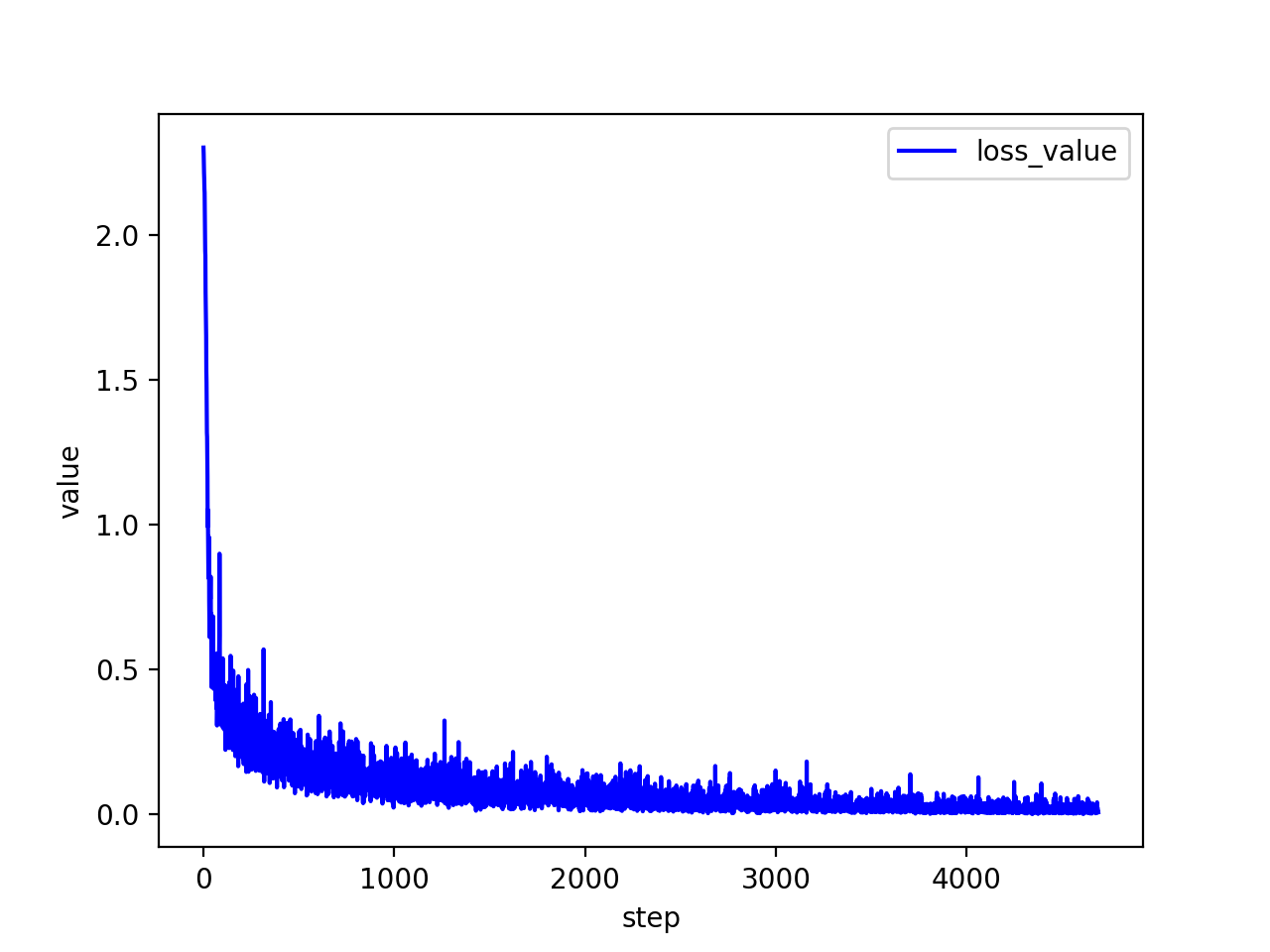
可见，训练轮数越多，损失函数值越低，波动越小。

3.3 实验 3

这次，我们调大批处理时每批数据的规模（batch_size），观察预测准确率的变化。

3.3.1 参数

1
2
3

epoch_number = 10
batch_size = 256
learning_rate = 0.1

3.3.2 预测准确率

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

[0] Accuracy: 0.9253
[1] Accuracy: 0.9477
[2] Accuracy: 0.9522
[3] Accuracy: 0.9651
[4] Accuracy: 0.9680
[5] Accuracy: 0.9731
[6] Accuracy: 0.9755
[7] Accuracy: 0.9766
[8] Accuracy: 0.9766
[9] Accuracy: 0.9790

可见，每批数据的规模越大，训练速度越慢，但最终达到的准确率没有明显变化。

3.3.3 损失函数值

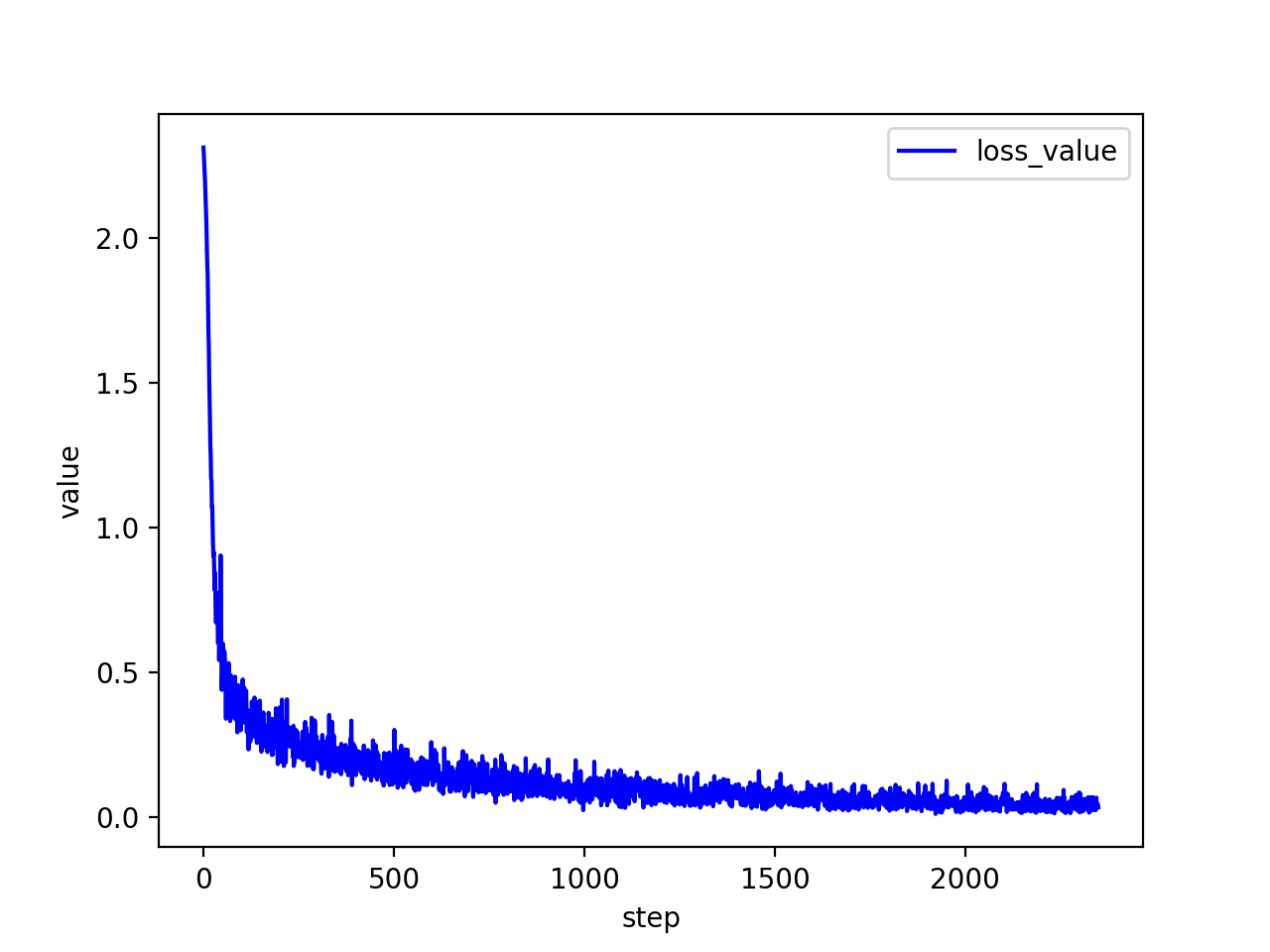
可见，每批数据的大小越大，损失函数值整体的波动越小。

3.4 实验 4

这次，我们提高学习率（learning_rate），观察预测准确率的变化。

3.4.1 参数

1
2
3

epoch_number = 10
batch_size = 256
learning_rate = 0.5

3.4.2 预测准确率

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

[0] Accuracy: 0.9505
[1] Accuracy: 0.9675
[2] Accuracy: 0.9706
[3] Accuracy: 0.9471
[4] Accuracy: 0.9737
[5] Accuracy: 0.8980
[6] Accuracy: 0.9757
[7] Accuracy: 0.9573
[8] Accuracy: 0.9770
[9] Accuracy: 0.9792

可见，学习率越高，训练速度越快，但训练时的波动也可能较大。

3.4.3 损失函数值

可见，学习率越高，损失函数值下降越快，但整体的波动也可能较大。