Hakula.XYZ
Hakula.XYZ

目录

https://hakula-1257872502.file.myqcloud.com/images/article-covers/90743556.webp

PRML - Lab 1: KNN 算法

Hakula收录于 笔记
约 2662 字 预计阅读 6 分钟 0 次阅读

本次作业利用 NumPy 实现了一个 KNN 模型。

Pattern Recognition and Machine Learning (H) @ Fudan University, spring 2021.

封面出处
行くよ。 - @SWAV
源码地址
  Hakula / prml-21-spring / assignment-1

实验简介

参见
Hakula / prml-21-spring / assignment-1 / README.md - Gitee

实验报告

1 KNN 模型实现

KNN 算法（$k$-nearest neighbors algorithm）的主要思路是：根据当前点 $P_0$ 最近的 $k$ 个邻居 $P$ 的标签，选择其中出现频率最高的标签，作为 $P_0$ 标签的预测结果。

具体来说，我们使用函数 _distance 获取两点间的距离。

def _distance(p1: np.ndarray, p2: np.ndarray, mode: int = 2) -> float:
    '''
    Get the distance between two points.

    :param `p1`: the first point
    :param `p2`: the second point
    :param `mode`: which exponent to use when calculating distance,
                   using `2` by default for Euclidean distance
    '''

    assert p1.shape == p2.shape, (
        '_distance: dimensions not match for '
        f'{p1.shape} and {p2.shape}'
    )
    return np.linalg.norm(p1 - p2, ord=mode)

这里我们使用了 numpy 库提供的 np.linalg.norm 方法来获取两点间的距离。特别地，当参数 ord 为 2 时，即采用 Euclidean 距离。我们这里使用 2 作为默认参数。

接下来，我们维护一个大小为 $k$ 的最小堆，来得到最近的 $k$ 个邻居。思想就是 top k 问题的经典算法。

def _get_k_nearest_neighbors(
    self, k: int, base_p: np.ndarray, dataset: int = Dataset.TRAIN_SET
) -> List[int]:
    '''
    Get k nearest neighbors of a point from dataset. Each point (except the
    base point) is denoted by its index in the dataset.

    :param `base_p`: the base point
    :param `dataset`: which dataset to use
    '''

    if dataset == Dataset.TRAIN_SET:
        data = self.train_data
    elif dataset == Dataset.DEV_SET:
        data = self.dev_data
    else:
        data = self.test_data

    # Use a min heap of size k to get the k nearest neighbors
    heap: List[Tuple[float, np.ndarray]] = []
    for p_i in range(data.shape[0]):
        dist: float = _distance(base_p, data[p_i])
        if (len(heap) < k):
            heappush(heap, (-dist, p_i))
        else:
            heappushpop(heap, (-dist, p_i))

    # Return the indices of the k points in the dataset
    return [item[1] for item in heap]

最后我们对这 $k$ 个邻居的标签分别进行计数，选择其中出现次数最多的标签作为预测结果。

def _get_most_common_label(
    self, labels_i: List[int], dataset: int = Dataset.TRAIN_SET
) -> int:
    '''
    Get the most common label in given labels. Each label is denoted by
    its data point's index in the dataset.

    :param `labels_i`: the indices of given labels
    :param `dataset`: which dataset to use
    '''

    if dataset == Dataset.TRAIN_SET:
        all_labels = self.train_label
    else:
        all_labels = self.dev_label

    labels: List[int] = [all_labels[i] for i in labels_i]
    return max(set(labels), key=labels.count)

训练模型时，我们先将数据集打乱，然后将其中的 $75\%$ 作为训练集 train_data，剩下 $25\%$ 作为验证集 dev_data，然后使用 KNN 算法进行训练。我们选择不同的 $k$ 值，通过比较验证集 dev_data 的预测结果和其实际标签 dev_label，得到每个 $k$ 值所对应的预测准确率 accuracy。最终，我们选择准确率最高的 $k$ 值作为测试集 test_data 上使用的参数 $k$。

def fit(self, train_data: np.ndarray, train_label: np.ndarray) -> None:
    '''
    Train the model using a training set with labels.

    :param `train_data`: training set
    :param `train_label`: provided labels for data in training set
    '''

    # Shuffle the dataset with labels
    assert train_data.shape[0] == train_label.shape[0], (
        'fit: data size not match for '
        f'{train_data.shape[0]} and {train_label.shape[0]}'
    )
    shuffled_i = np.random.permutation(train_data.shape[0])
    shuffled_data: np.ndarray = train_data[shuffled_i]
    shuffled_label: np.ndarray = train_label[shuffled_i]

    # Separate training set and development set (for validation)
    train_ratio: float = 0.75
    train_size: int = floor(shuffled_data.shape[0] * train_ratio)
    self.train_data = shuffled_data[:train_size]
    self.train_label = shuffled_label[:train_size]
    self.dev_data = shuffled_data[train_size:]
    self.dev_label = shuffled_label[train_size:]

    print('=== Training ===')

    # Compare the predicted and expected results, calculate the accuracy
    # for each parameter k, and find out the best k for prediction.
    k_threshold: int = train_size if train_size < 20 else 20
    accuracy_table: List[float] = [0.0]
    max_accuracy: float = 0.0

    for k in range(1, k_threshold):
        predicted_labels: List[int] = []
        for p in self.dev_data:
            k_nearest_neighbors: List[int] = self._get_k_nearest_neighbors(
                k, p, Dataset.TRAIN_SET
            )
            predicted_label: int = self._get_most_common_label(
                k_nearest_neighbors, Dataset.TRAIN_SET
            )
            predicted_labels.append(predicted_label)
        prediction: np.ndarray = np.array(predicted_labels)

        accuracy: float = np.mean(np.equal(prediction, self.dev_label))
        accuracy_table.append(accuracy)
        print(f'k = {k}, train_acc = {accuracy * 100} %')
        if accuracy > max_accuracy:
            max_accuracy, self.k = accuracy, k

    print(f'best k = {self.k}\n')

对测试集进行预测时，我们就使用之前得到的最优的参数 $k$ 进行预测，同样使用 KNN 算法。

def predict(self, test_data: np.ndarray) -> np.ndarray:
    '''
    Predict the label of a point using our model.

    :param `test_data`: testing set
    '''

    self.test_data = test_data

    print('=== Predicting ===')

    predicted_labels: List[int] = []
    for p in self.test_data:
        k_nearest_neighbors: List[int] = self._get_k_nearest_neighbors(
            self.k, p, Dataset.TRAIN_SET
        )
        predicted_label: int = self._get_most_common_label(
            k_nearest_neighbors, Dataset.TRAIN_SET
        )
        predicted_labels.append(predicted_label)
    prediction: np.ndarray = np.array(predicted_labels)
    return prediction

2 生成数据

我们使用不同的参数生成数据集，并保存到文件 data.npy。这里由于时间有限，为了方便起见，我们直接在函数 generate 的 parameters 变量中进行参数的修改。

def generate() -> None:
    '''
    Generate datasets using different parameters, and save to a file for
    further use.
    '''

    class Parameter(NamedTuple):
        mean: Tuple[int, int]
        cov: List[List[float]]
        size: int
        label: int

    def _generate_with_parameters(param: Parameter) -> np.ndarray:
        '''
        Generate a dataset using given parameters.

        :param `param`: a tuple of `mean`, `cov`, `size`
            `mean`: the mean of the dataset
            `cov`: the coefficient of variation (COV) of the dataset
            `size`: the number of points in the dataset
        '''

        return np.random.multivariate_normal(
            param.mean,
            param.cov,
            param.size,
        )

    parameters: List[Parameter] = [
        Parameter(
            mean=(1, 2),
            cov=[[73, 0], [0, 22]],
            size=800,
            label=0,
        ),
        Parameter(
            mean=(16, -5),
            cov=[[21.2, 0], [0, 32.1]],
            size=200,
            label=1,
        ),
        Parameter(
            mean=(10, 22),
            cov=[[10, 5], [5, 10]],
            size=1000,
            label=2,
        ),
    ]

    data: List[np.ndarray] = [
        _generate_with_parameters(param) for param in parameters
    ]

    indices: np.ndarray = np.arange(2000)
    np.random.shuffle(indices)
    all_data: np.ndarray = np.concatenate(data)
    all_label = np.concatenate([
        np.ones(param.size, int) * param.label for param in parameters
    ])
    shuffled_data: np.ndarray = all_data[indices]
    shuffled_label: np.ndarray = all_label[indices]

    train_data: np.ndarray = shuffled_data[:1600]
    train_label: np.ndarray = shuffled_label[:1600]
    test_data: np.ndarray = shuffled_data[1600:]
    test_label: np.ndarray = shuffled_label[1600:]
    np.save('data.npy', (
        (train_data, train_label),
        (test_data, test_label),
    ))

为了直观起见，我们提供了函数 display 用于将当前使用的数据集可视化，并将图片保存到 img 目录下。

def display(data: np.ndarray, label: np.ndarray, name: str) -> None:
    '''
    Visualize dataset with labels using `matplotlib.pyplot`.

    :param `data`: dataset
    :param `label`: labels for data in the dataset
    :param `name`: file name when saving to file
    '''

    datasets_with_label: List[List[np.ndarray]] = [[], [], []]
    for i in range(data.shape[0]):
        datasets_with_label[label[i]].append(data[i])

    for dataset_with_label in datasets_with_label:
        dataset_with_label_: np.ndarray = np.array(dataset_with_label)
        plt.scatter(dataset_with_label_[:, 0], dataset_with_label_[:, 1])

    plt.savefig(f'img/{name}')
    plt.show()

3 运行代码

在当前目录下，我们可以使用以下参数执行代码 source.py，具体功能参见注释。

# 训练模型及预测
python ./source.py g

# 展示数据集
python ./source.py d

3.1 输出样例

=== Training ===
k = 1, train_acc = 67.5 %
k = 2, train_acc = 67.75 %
k = 3, train_acc = 70.5 %
k = 4, train_acc = 72.5 %
k = 5, train_acc = 72.75 %
k = 6, train_acc = 73.25 %
k = 7, train_acc = 74.25 %
k = 8, train_acc = 74.0 %
k = 9, train_acc = 75.75 %
k = 10, train_acc = 75.5 %
k = 11, train_acc = 75.75 %
k = 12, train_acc = 75.5 %
k = 13, train_acc = 75.75 %
k = 14, train_acc = 75.5 %
k = 15, train_acc = 75.5 %
k = 16, train_acc = 74.5 %
k = 17, train_acc = 75.0 %
k = 18, train_acc = 75.0 %
k = 19, train_acc = 75.25 %
best k = 9

=== Predicting ===
k = 9, predict_acc = 71.5 %

4 实验探究

4.1 实验 1

4.1.1 参数
mean = (1, 2)
cov = [[73, 0], [0, 22]]
size = 800
mean = (16, -5)
cov = [[21.2, 0], [0, 32.1]]
size = 200
mean = (10, 22)
cov = [[10, 5], [5, 10]]
size = 1000

其中：

  • mean 表示数据集的均值
  • cov 表示数据集的协方差
  • size 表示数据集的大小
4.1.2 数据集
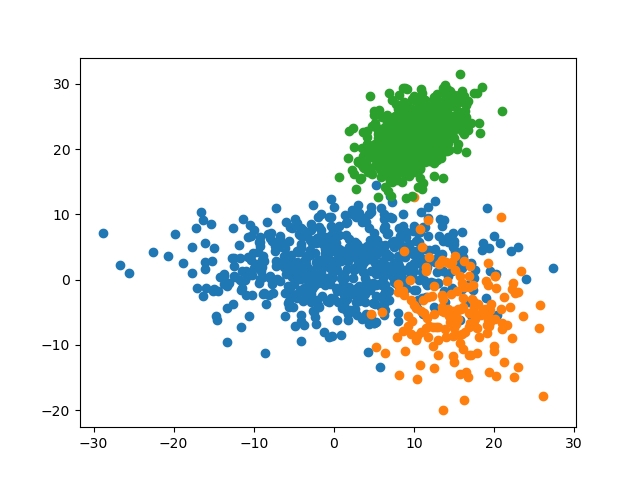
/posts/note/prml/knn/assets/1-train.webp
实验 1 - 训练集
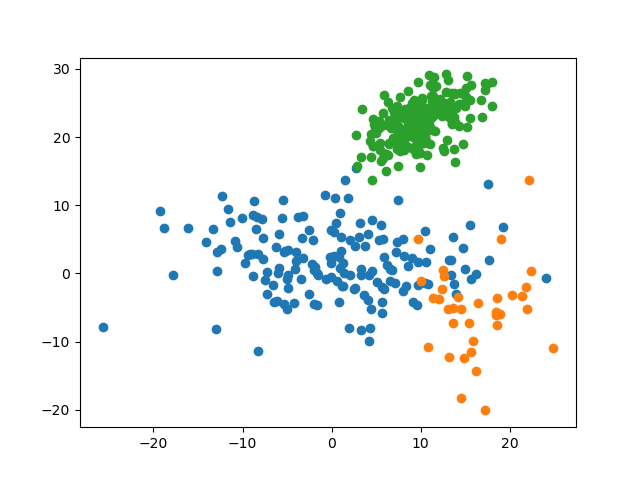
/posts/note/prml/knn/assets/1-test.webp
实验 1 - 测试集
4.1.3 预测准确率

训练时使用的参数 $k$ 及相应的准确率如下所示：

k = 1, train_acc = 95.75 %
k = 2, train_acc = 95.75 %
k = 3, train_acc = 97.25 %
k = 4, train_acc = 96.25 %
k = 5, train_acc = 96.5 %
k = 6, train_acc = 96.5 %
k = 7, train_acc = 96.75 %
k = 8, train_acc = 96.75 %
k = 9, train_acc = 96.75 %
k = 10, train_acc = 96.5 %
k = 11, train_acc = 96.5 %
k = 12, train_acc = 96.5 %
k = 13, train_acc = 96.75 %
k = 14, train_acc = 97.0 %
k = 15, train_acc = 96.75 %
k = 16, train_acc = 96.75 %
k = 17, train_acc = 96.75 %
k = 18, train_acc = 96.75 %
k = 19, train_acc = 97.0 %

预测时使用的参数 $k$ 及相应的准确率如下所示：

k = 3, predict_acc = 96.0 %

可见，对于此数据集，最优的参数 $k$ 为 $3$，其对测试集的预测准确率为 $96.0\%$。

4.2 实验 2

这次，我们调大数据集之间的距离，观察预测准确率的变化。

4.2.1 参数
mean = (-5, 2)
cov = [[73, 0], [0, 22]]
size = 800
mean = (30, -10)
cov = [[21.2, 0], [0, 32.1]]
size = 200
mean = (20, 40)
cov = [[10, 5], [5, 10]]
size = 1000
4.2.2 数据集
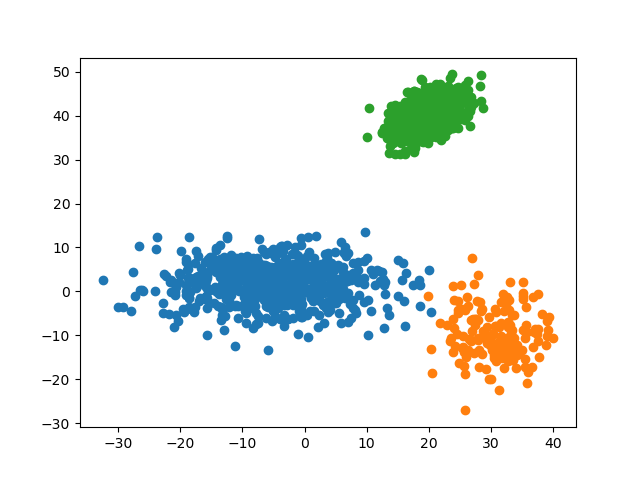
/posts/note/prml/knn/assets/2-train.webp
实验 2 - 训练集
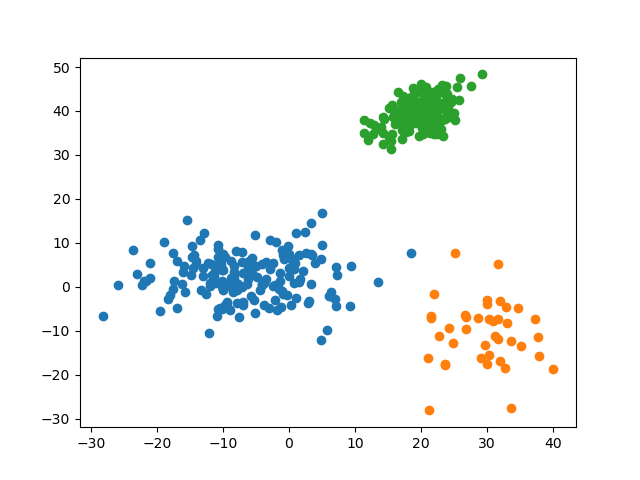
/posts/note/prml/knn/assets/2-test.webp
实验 2 - 测试集
4.2.3 预测准确率

训练时使用的参数 $k$ 及相应的准确率如下所示：

k = 1, train_acc = 100.0 %
k = 2, train_acc = 100.0 %
k = 3, train_acc = 100.0 %
k = 4, train_acc = 100.0 %
k = 5, train_acc = 100.0 %
k = 6, train_acc = 100.0 %
k = 7, train_acc = 100.0 %
k = 8, train_acc = 100.0 %
k = 9, train_acc = 100.0 %
k = 10, train_acc = 100.0 %
k = 11, train_acc = 100.0 %
k = 12, train_acc = 100.0 %
k = 13, train_acc = 100.0 %
k = 14, train_acc = 100.0 %
k = 15, train_acc = 100.0 %
k = 16, train_acc = 100.0 %
k = 17, train_acc = 100.0 %
k = 18, train_acc = 100.0 %
k = 19, train_acc = 100.0 %

预测时使用的参数 $k$ 及相应的准确率如下所示：

k = 1, predict_acc = 100.0 %

可见，对于不同标签区分度较大（即彼此间距离较远）的数据集，所有 $k$ 的预测准确率均为 $100.0\%$。这说明 KNN 算法对于较分散的数据有着很高的准确率。

4.3 实验 3

我们再试试减小数据集间的距离，观察预测准确率的变化。

4.3.1 参数
mean = (1, 2)
cov = [[73, 0], [0, 22]]
size = 800
mean = (3, -2)
cov = [[21.2, 0], [0, 32.1]]
size = 200
mean = (-5, 4)
cov = [[10, 5], [5, 10]]
size = 1000
4.3.2 数据集
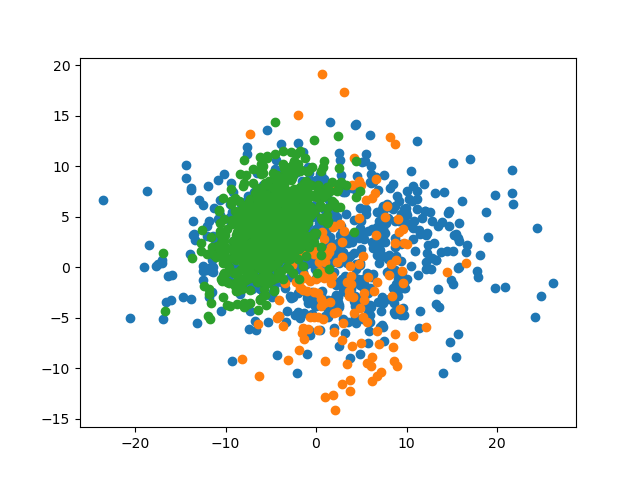
/posts/note/prml/knn/assets/3-train.webp
实验 3 - 训练集
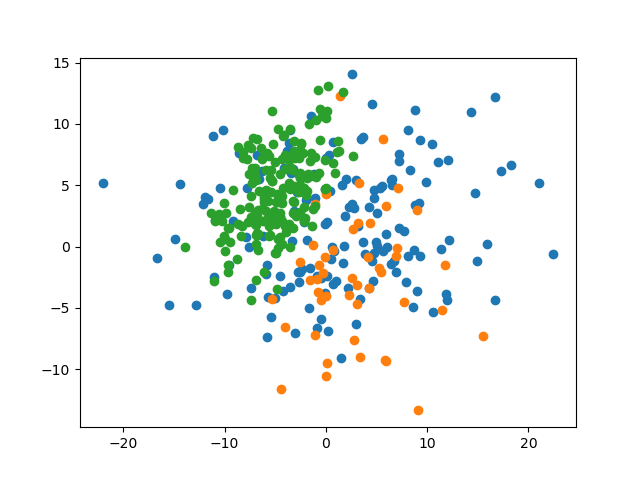
/posts/note/prml/knn/assets/3-test.webp
实验 3 - 测试集
4.3.3 预测准确率

训练时使用的参数 $k$ 及相应的准确率如下所示：

k = 1, train_acc = 65.0 %
k = 2, train_acc = 65.75 %
k = 3, train_acc = 69.25 %
k = 4, train_acc = 68.25 %
k = 5, train_acc = 72.5 %
k = 6, train_acc = 71.5 %
k = 7, train_acc = 73.75 %
k = 8, train_acc = 75.0 %
k = 9, train_acc = 76.0 %
k = 10, train_acc = 75.75 %
k = 11, train_acc = 76.0 %
k = 12, train_acc = 74.5 %
k = 13, train_acc = 75.25 %
k = 14, train_acc = 75.0 %
k = 15, train_acc = 74.75 %
k = 16, train_acc = 75.5 %
k = 17, train_acc = 75.0 %
k = 18, train_acc = 75.0 %
k = 19, train_acc = 74.5 %

预测时使用的参数 $k$ 及相应的准确率如下所示：

k = 9, predict_acc = 76.0 %

此时，最优的参数 $k$ 为 $9$，其对测试集的预测准确率为 $76.0\%$。可见，当数据集间的区分度较低时，较高的 $k$ 值有着相对较高的准确率。这是可以理解的，因为提高可参考的邻居数量可以尽可能地减少噪声的影响。

更新于 2023-06-30  cec8b1a
CC BY-NC-SA 4.0
PRML, 机器学习, KNN, NumPy, Python
返回 | 主页