
CS:APP - Data Lab
Introduction to Computer Systems I (H) @ Fudan University, fall 2019.
实验简介
实验报告
1 bitAnd
x & y using only ~ and |.1.1 思路
利用 De Morgan’s laws 即可。
1.2 解答
int bitAnd(int x, int y) {
/* De Morgan's laws */
return ~((~x) | (~y));
}2 getByte
2.1 思路
$1\ \mathrm{byte} = 8\ \mathrm{bit}$,因此将 $x$ 右移 $8n$ 位后,$x$ 最低的字节就是我们需要提取的 byte $n$。之后利用掩码 $\mathtt{0xFF}$ 提取即可。
2.2 解答
int getByte(int x, int n) {
/* x AND 0xff returns the lowest byte of x. */
return (x >> (n << 3)) & 0xff;
}3 logicalShift
3.1 思路
负数右移时会在高位补 $1$,因此需要用掩码提取最低的 $(32-n)$ 位。这里将 $\mathtt{0x1}$ 左移 $31$ 位到最高位,然后右移 $(n-1)$ 位得到一个高位 $n$ 个 $1$、低位 $(32-n)$ 个 $0$ 的二进制数,最后取反即得到我们所需的掩码。
3.2 解答
int logicalShift(int x, int n) {
/*
* Mask the highest n bits after doing right shifts,
* especially for negative numbers.
*/
int mask = ~(((0x1 << 31) >> n) << 1);
return (x >> n) & mask;
}4 bitCount
4.1 思路
因为不允许使用循环遍历,这里采用了分治法的思想。1
我们先将这 $32$ 位数分成左右两组,每组 $16$ 位;然后将每组 $16$ 位数再分成左右两组,每组 $8$ 位数;以此类推,一直细分到每组 $1$ 位数。
我们知道每组中 $1$ 的个数 $=$ 左组 $1$ 的个数 $+$ 右组 $1$ 的个数,因此只要每次将相邻的左组加到右组上,即可得到这组中 $1$ 的个数。而对于最开始只有 $1$ 位数的组,其中 $1$ 的个数就等于这个数本身。
例如:
1 0 1 1 0 0 0 1
=> 1+0 1+1 0+0 0+1
=> 01 +10 00 +01
=> 0011 +0001
=> 00000100 (= 4)在具体实现中,由于常数限定在 $[\mathtt{0x0},\mathtt{0xFF}]$ 的范围,因此做了一些额外处理。
4.2 解答
int bitCount(int x) {
/* Add adjacent bits together each time. */
int mask16 = 0x55 | (0x55 << 8);
int mask8 = 0x33 | (0x33 << 8);
int mask4 = 0x0f | (0x0f << 8);
int mask2 = 0xff | (0xff << 16);
int mask1 = 0xff | (0xff << 8);
mask16 = mask16 | (mask16 << 16);
mask8 = mask8 | (mask8 << 16);
mask4 = mask4 | (mask4 << 16);
x = (x & mask16) + ((x >> 1) & mask16);
x = (x & mask8) + ((x >> 2) & mask8);
x = (x & mask4) + ((x >> 4) & mask4);
x = (x & mask2) + ((x >> 8) & mask2);
x = (x & mask1) + ((x >> 16) & mask1);
return x;
}5 bang
!x without using !.5.1 思路
只需判断原数是否为 $0$。这里将 $x$ 每次压缩成原来位数的一半,用 $\mathrm{OR}$ 运算来保留所有的 $1$。如果最终得到的 $1$ 位数为 $0$ 即表示 $x = 0$,否则 $x\ne 0$。最后取反并利用掩码 $\mathtt{0x1}$ 提取结果即可。
5.2 解答
int bang(int x) {
/* Compress the original number to 1 bit. */
x = x | (x >> 16);
x = x | (x >> 8);
x = x | (x >> 4);
x = x | (x >> 2);
x = x | (x >> 1);
return (~x) & 0x1;
}6 tmin
6.1 思路
由二补码的规则易知 $\mathrm{tmin} = \mathtt{0x80000000}$。由于常数限定在 $[\mathtt{0x0},\mathtt{0xFF}]$ 的范围,因此采用 0x1 << 31 来表示。
6.2 解答
int tmin(void) {
/* tmin = 0x80000000 */
return 0x1 << 31;
}7 fitsBits
7.1 思路
如果一个非负数 $x$ 可以表示成 $n$ 位二补码的形式,那么 $x$ 最高的 $1$ 必然不能高于第 $(n-1)$ 位。因此如果对 $x$ 右移 $(n-1)$ 位所得的结果为 $0$,即表示 $x$ 是符合要求的。
为了方便起见,将负数直接取反。如果取反后的 $\mathrm{NOT}\ x$ 能表示成 $n$ 位二补码的形式,那么 $x$ 也同样能表示。这是因为 $x$ 的范围 $[\mathtt{0x80000000},\mathtt{0xFFFFFFFF}]$ 与 $\mathrm{NOT}\ x$ 的范围 $[\mathtt{0x00000000},\mathtt{0x7FFFFFFF}]$ 一一对应,而后者正是非负数的范围。
因为不允许使用条件语句,如何将负数取反的同时保持正数不变,这里用了一个 trick,详见代码部分。因为不允许使用减号,这里就用 $\mathrm{NOT}\ 0$ 来表示 $-1$ 了。
7.2 解答
int fitsBits(int x, int n) {
/*
* Convert x to a non-negative number in advance for convenience. If a
* non-negative number can be represented as an n-bit, two's complement
* integer, it should become 0 after doing right shift by (n - 1) times.
*/
int sign = x >> 31;
x = (x & ~sign) + (~x & sign); // x = x < 0 ? ~x : x;
return !(x >> (n + ~0));
}8 divpwr2
8.1 思路
非负数直接右移即可;负数直接右移会向下取整,但要求是向 $0$ 取整(向上取整),因此需要加上一个偏移量。具体处理方式类似于十进制里对进一法的处理,即在原数上先加 $2^n - 1$,这样即可确保右移 $n$ 位后的结果是向上取整。
8.2 解答
int divpwr2(int x, int n) {
/*
* Positive numbers: x >> n
* Negative numbers: (x + (1 << n) - 1) >> n (to round toward 0)
*/
int sign = x >> 31;
int offset = sign & ((0x1 << n) + ~0);
return (x + offset) >> n;
}9 negate
9.1 思路
取反加一即可。
9.2 解答
int negate(int x) {
return ~x + 1;
}10 isPositive
10.1 思路
关键在于对 $0$ 的处理,直接返回 !(x >> 31) 对于 $0$ 是错误的。
我们发现:
| 正数 | 负数 | 0 | |
|---|---|---|---|
!(x >> 31) | 1 | 0 | 1 |
!x | 0 | 0 | 1 |
| 期望结果 | 1 | 0 | 0 |
可见这里存在一个 $\mathrm{XOR}$ 的关系,于是就得到解答。
10.2 解答
int isPositive(int x) {
/*
* Positive numbers: !(x >> 31) = 1, !x = 0, expected 1
* Negative numbers: !(x >> 31) = 0, !x = 0, expected 0
* Zero: !(x >> 31) = 1, !x = 1, expected 0
*/
return (!(x >> 31)) ^ (!x);
}11 isLessOrEqual
11.1 思路
首先判断 $x$ 和 $y$ 的符号是否相同,因为如果符号不同,相减可能导致溢出问题,从而得出错误的结果。
如果 $x$ 和 $y$ 同号,那么 $y-x$ 不会导致溢出,我们判断 $y-x$ 的符号即可。如果 $y-x$ 为非负数则结果为真,否则为假。
如果 $x$ 和 $y$ 异号,那么负数必然小于非负数,我们判断 $x$ 的符号即可。如果 $x$ 为负数则结果为真,否则为假。
11.2 解答
int isLessOrEqual(int x, int y) {
/*
* If x and y have the same sign, judge the sign of (y - x);
* otherwise, the negative one is smaller than the positive one.
*/
int sign_diff = x ^ y;
int diff = y + ~x + 1;
return (((sign_diff & x) | (~sign_diff & ~diff)) >> 31) & 0x1;
}12 ilog2
12.1 思路
目标是找到 $x$ 最高的 $1$ 所在的位置。
因为不允许使用循环遍历,这里采用二分查找1,详见代码部分。
12.2 解答
int ilog2(int x) {
/* Find the highest 1 in x through binary search. */
int result = (!!(x >> 16)) << 4;
result += (!!(x >> (result + 8))) << 3;
result += (!!(x >> (result + 4))) << 2;
result += (!!(x >> (result + 2))) << 1;
result += (!!(x >> (result + 1)));
return result;
}13 float_neg
Return bit-level equivalent of expression $-f$ for floating point argument $f$.
Both the argument and result are passed as unsigned int’s, but they are to be interpreted as the bit-level representations of single-precision floating point values.
When argument is $\mathrm{NaN}$, return argument.
13.1 思路
关键在于判断原数是否为 $\mathrm{NaN}$,是则直接返回,否则将符号位(最高位)取反后返回。
当 $f$ 的 exponent bits 全为 $1$ 且 fraction bits 不全为 $0$ 时,$f$ 即为 $\mathrm{NaN}$。2
13.2 解答
unsigned float_neg(unsigned uf) {
/*
* If uf is NaN, return uf;
* otherwise, convert the sign bit to the opposite.
*/
unsigned sign_mask = 0x1 << 31;
unsigned exp_mask = 0xff << 23;
unsigned frac_mask = 0x7fffff;
unsigned exp = uf & exp_mask;
unsigned frac = uf & frac_mask;
if (exp == exp_mask && frac) return uf; // uf is NaN
return uf ^ sign_mask;
}14 float_i2f
Return bit-level equivalent of expression (float) x.
Result is returned as unsigned int, but it is to be interpreted as the bit-level representation of a single-precision floating point values.
14.1 思路
为了方便起见,先将负数转化为其相反数。为此需要将 INT_MIN($\mathtt{0x80000000}$)作为特殊情况处理。同时由于整数中只有 $0$ 是 subnormal number2,因此也作为特殊情况处理。
此后先将 fraction bits 顶到最高位,这样做的好处是之后将有效位数部分截断时,方便判断是否需要进位。
而本题的关键正是这个进位判断。需要注意的是,二进制进位时不是只看被舍去部分的最高位,而是整个被舍去部分(有时也可以只看最高两位)和被保留部分的最低位。在本题中,因为已经将 fraction bits 顶到最高位,因此最低 $8$ 位就是被舍去的部分($32$ 位数中,fraction bits 最多只能有 $23$ 位)。于是,进位判断的条件为:
- 如果被舍去部分大于 $\mathtt{0x80}$,则需要进位;
- 如果被舍去部分等于 $\mathtt{0x80}$,且被保留部分最低位为 $1$,则需要进位;
- 其余情况不进位。
解决了进位问题后,其余问题都不是问题,详见代码部分。
14.2 解答
unsigned float_i2f(int x) {
unsigned int_min = 0x80000000;
unsigned exp = 31;
unsigned carry = 0;
unsigned new_x = 0;
/* Deal with special cases. */
if (x == 0) return 0;
if (x == int_min) return 0xcf000000;
/* Convert x to positive for convenience. */
if (x < 0) {
x = -x;
/* Set the sign bit. */
new_x |= int_min;
}
/* Move the fraction bits to the top. */
while (!(x & int_min)) {
x <<= 1;
--exp;
}
/* Set the exponent bits. */
new_x |= (exp + 127) << 23;
/* Judge whether carry is 0 or 1. */
if ((x & 0x1ff) == 0x180 || (x & 0xff) > 0x80) carry = 1;
// else carry = 0;
/* Set the fraction bits. */
new_x |= (x >> 8) & 0x7fffff;
new_x += carry;
return new_x;
}15 float_twice
Return bit-level equivalent of expression $2f$ for floating point argument $f$.
Both the argument and result are passed as unsigned int’s, but they are to be interpreted as the bit-level representation of single-precision floating point values.
When argument is $\mathrm{NaN}$, return argument.
15.1 思路
只需要处理一些特殊情况即可。
- 当 $f$ 是 $\pm 0$ 时,直接返回;
- 当 $f$ 是 $\mathrm{NaN}$ 时,直接返回;
- 当 $f$ 是 subnormal number 时,直接将 fraction bits 左移 $1$ 位后返回3;
- 其余情况,将 exponent bits 加 $1$。
15.2 解答
unsigned float_twice(unsigned uf) {
/* Deal with special cases. */
unsigned sign_mask = 0x1 << 31;
unsigned exp_mask = 0xff << 23;
unsigned sign = uf & sign_mask;
unsigned exp = uf & exp_mask;
if (uf == 0 || uf == sign_mask) return uf; // uf is +0 / -0
if (exp == exp_mask) return uf; // uf is NaN
if (exp == 0) return (uf << 1) | sign; // uf is a subnormal number
return uf + (0x1 << 23);
}运行结果
dlc
./dlc bits.c
./dlc bits.c -e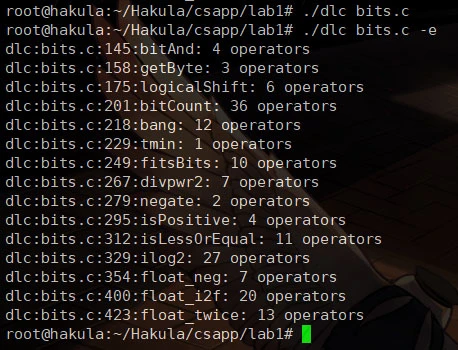
btest
./btest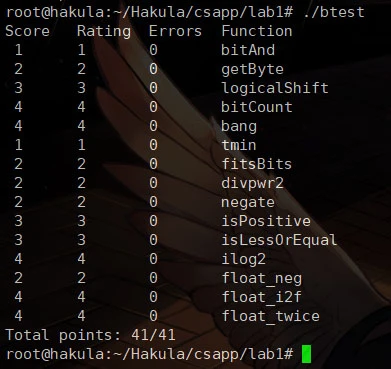
测试环境
- Ubuntu 18.04.3 LTS (GNU/Linux 5.0.0-29-generic x86_64)
- GCC 7.4.0
- GNU Make 4.1
心得体会
有几个题确实难,想了几个小时都想不出来,只好去参考网上的思路。其实从学习效率的角度,感觉毫无头绪的题,在那边硬想也只不过是一种「自我感动」的浪费时间。做这个 Lab 总共耗时 3 天,其中不少时间就是这样无意义地浪费掉了,很不值得。